(WIP) Learning to Learn (Efficient ML Seminar Series)

May 03, 2024

2024   ·   efficient-ml-seminar     ·   notes  

Taking notes on stuff I watch/listen/read in public and trying it for size! Feel free to email me any feedback you have: this is something new-ish for me, so any feedback is extremely welcome!

This blog consists of some of my notes on the “Learning To Learn” seminar of the Harvard Efficient ML Seminar Series: You can find a recording of the seminar here. Try clicking some of the images to jump to the recording of the talk!

Author Bios

The talk consisted of two portions: the first workshop was given by Julian Coda-Forno, an ELLIS Ph.D. student studying cognitive models for meta-reinforcement learning with interests also in studying LLMs from a cognitive neuroscience perspective. The tutorial was followed by a talk from Jane X. Wang, a staff researcher at Google Deepmind with a Ph.D. in applied physics at the University of Michigan who studies approaches to meta-learn in RL incorporating novel insights from cognitive neuroscience.

“Meta-learning in deep neural networks” (Julian Coda-Forno)

The “Harlow task” and an Introduction to Meta-Learning

Meta-learning as a field has most commonly originates from an experiment known as the “Harlow task” in 1949, capturing the fundamental phenomenon of cross-task generalization. For a given task, in each round, a subject is given a pair of two differently colored shapes randomly chosen side-by-side and, each round, selects the left or right shape, and, in turn, is given a reward. The subject needs to balance exploration with exploitation similar to a multi-armed bandit setting, as reward could be a function of the color, shape, or even whether it is left or right. Subjects go through multiple tasks where each task might have different types/colors of shapes: the commonality being only that each task has some hidden reward and two types of colored shapes shuffled to choose between. A smart enough agent should, after a trial of \(N\) tasks, achieve high or perfect accuracy on the second trial.

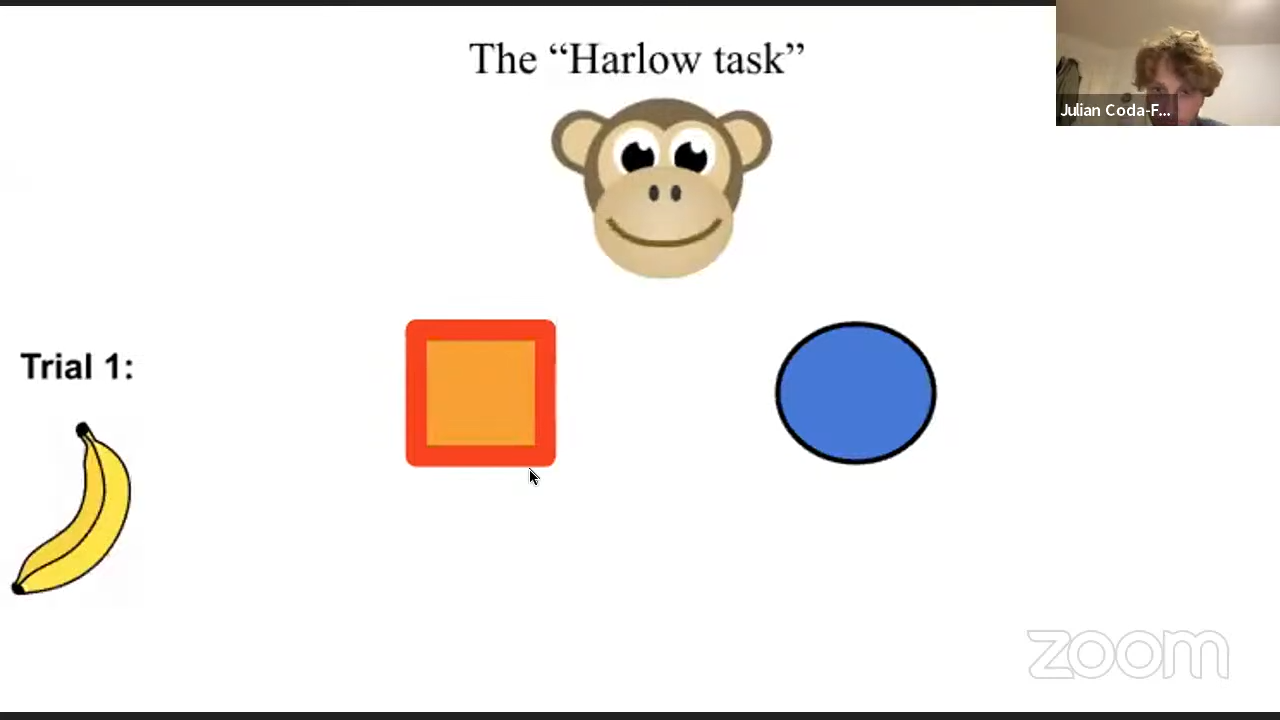
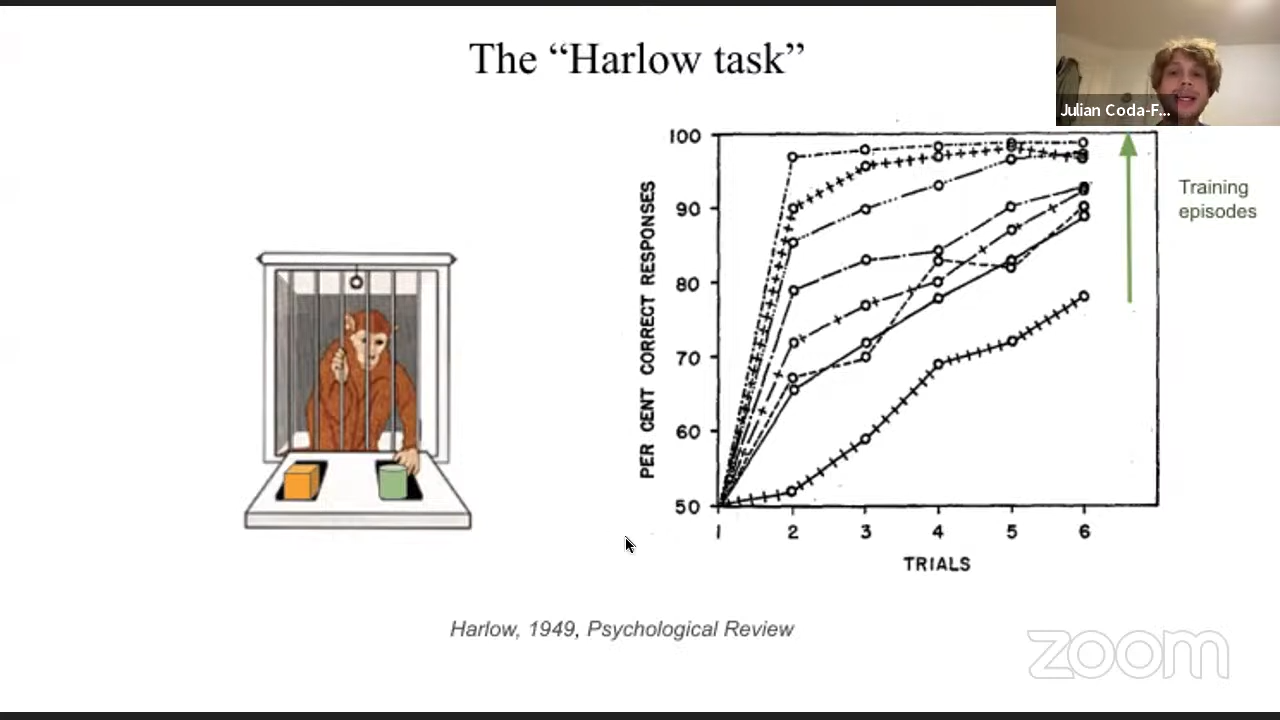
Harlow observed this phenomena when doing this experiment on monkeys, where they quickly achieved high accuracy after a few trials of multiple different tasks, indicating some level of cross-task generalization. He coined the term as the commonly used “learning to learn.”

More succinctly, Schaul and Schmidhuber (2010) define the process of an agent meta-learning as:

[using] its experience to change certain aspects of a learning algorithm, or the learning method itself, such that the modified learning is better than the original learning at learning from additional experience.

In more familiar terms, learning problems consist of examples in a single task that a learner computes a decision on: by computing through the learner’s parameters, minimizing some error and updating the learners parameters. Consequently, meta-learning consists of this process over multiple tasks, optimizing over what are called meta-parameters in which the performance measure on the tasks maximized and used to update the meta-parameters. You can imagine it more simply as a “inner loop” of the per-task learning on batches of a single task examples and the “outer loop” of the meta-learning over all tasks.

But what do meta-parameters actually correspond to in practice?

  • Doya (2002) present how the brain contains neuromodulatory systems that control the learning modules distributed elsewhere, explaining that these systems control things like memory update speed, stochasticity of action, and time scale and error of reward. This theory has been used widely downstream in machine learning to learn hyper-parameters like learning rate for base learning algorithms. The meta-parameters here are the hyper-parameters, while the parameters are the model itself.

  • Finn, Abbeel & Levine (2017) propose “model-agnostic meta-learning” (MAML) which seeks to train an initialization of a neural network that can quickly adapt to new tasks with few training steps. The authors achieve this by repeatedly sampling batches of different tasks and performing gradient descent over the entire batch of tasks rather than per task.

  • Baxter (1998) use meta-learning to learn a prior distribution: a learning begins with a “hyper-prior,” and using datasets from a training distribution, updates this to a “hyper-posterior” via Bayes rule. This “hyper-posterior” is then used as the prior for new tasks.

However, what if we want to meta-learn entire learning algorithms, also commonly termed as “black-box meta-learning”?

Black-box meta-learning

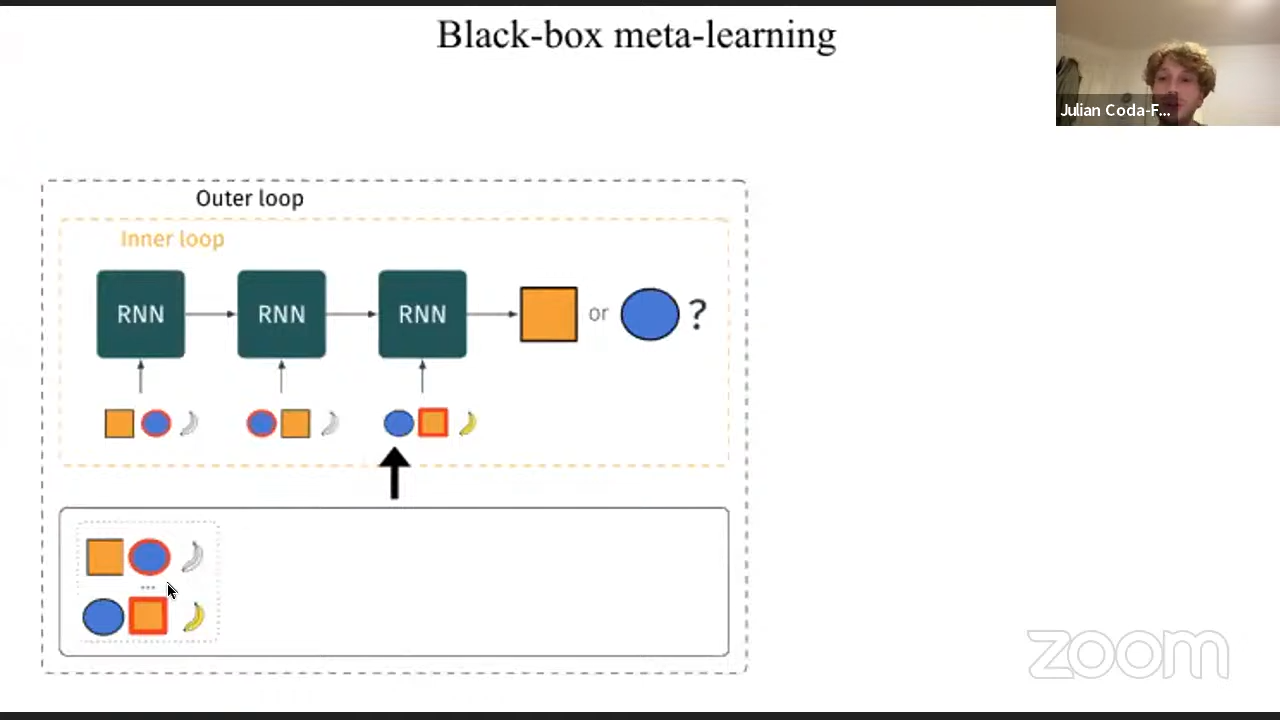
One common approach by Santoro et. al (2016) to do this is through a recurrent neural network (RNN). Going back to our shape tasks above, in a forward pass of this RNN, we compute the per-task learning “inner loop”: the idea here is that, given a task (two shapes and a hidden reward function) an RNN is trained on the sequence of previous observations: each recurrent unit input consists of the chosen shape and whether or reward was received. The final output of this RNN returns which shape to choose, where the “learning” in the forward pass consists of understanding from the history of observations what to choose next. The meta-learning “outer loop” is done by choosing different tasks at a time and backpropagating based on computed errors made by the RNNs.

Interestingly, Ortega et al. (2019) find that the inner learning loop, or the forward pass, implements Bayesian inference and has strong theoretical guarantees. In a related following work, Binz et al. (2023) show that the inner learning loop has three additional advantages:

  1. This method can implement Bayesian inference, even when computing exact posteriors is intractable. Computing posteriors from a prior is sometimes quite difficult, so keeping guarantees without having to exactly specify computation is quite neat.
  2. The Bayesian inference works when the inference priors/posteriors can’t be specified at all. As soon as we get to real world data in practice, this becomes very useful, as specifying likelihoods generally is restricted to toy problems.
  3. Meta-learning allows designer to exactly manipulate model complexity, allowing for things like reduced complexity for interpretability. etc. This also allows integration of neuro-scientific insights into models with this level of flexibility.

Summarized more succinctly, by McCoy and Griffiths:

meta-learning reconciles Bayesian approaches with connectionist models - thereby bringing together two successful research traditions tha have often been framed as antagonistic.

Applications of black-box meta-learning

Some key applications of black-box meta-learning include the below, listed and linked from the talk:

Meta-reinforcement learning

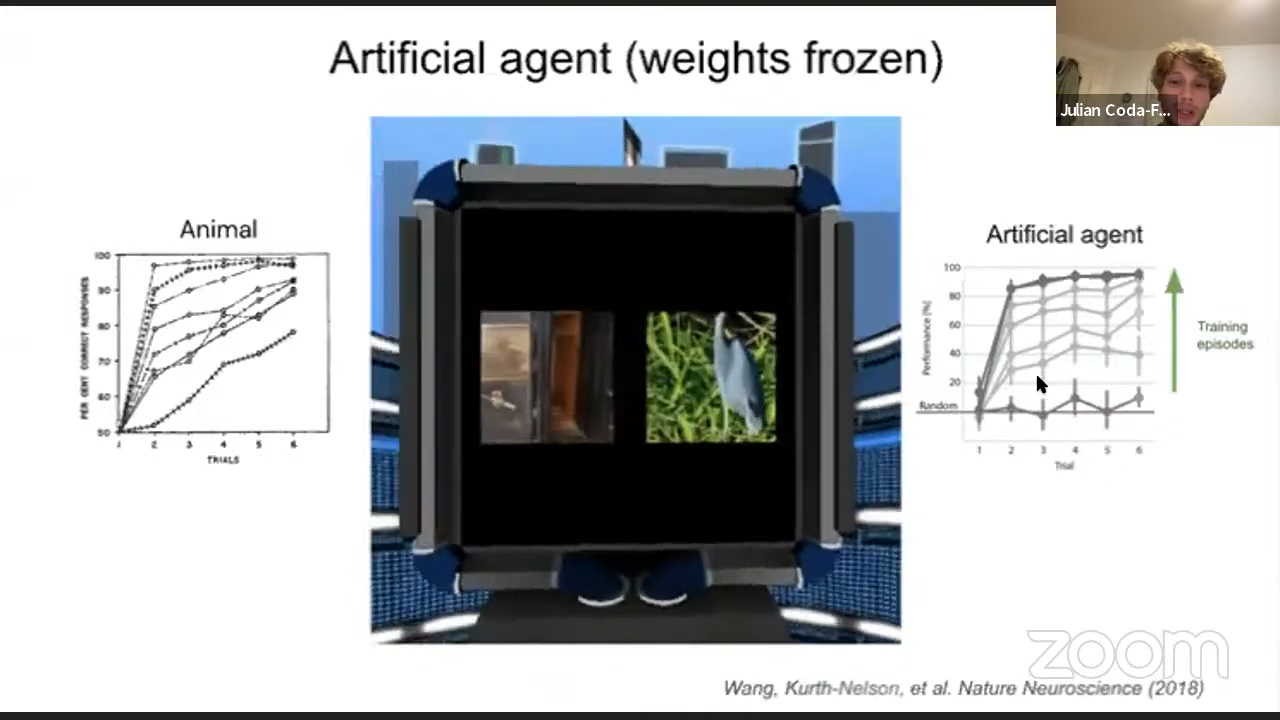
Specifically, going into more detail about meta-reinforcement learning: Wang et al. (2016) introduces RL algorithms for both the inner and outer loop. The inner loop corresponds to a task specific interaction with an environment: using an LSTM as a learner policy, which takes in a sequence states, actions and rewards. The weights of the LSTM are trained via policy gradient, and the outer loop consists of training the inner loop on several distributions of environments. Summarizing results, the authors achieve strong sample efficiency due to cross task generalization.

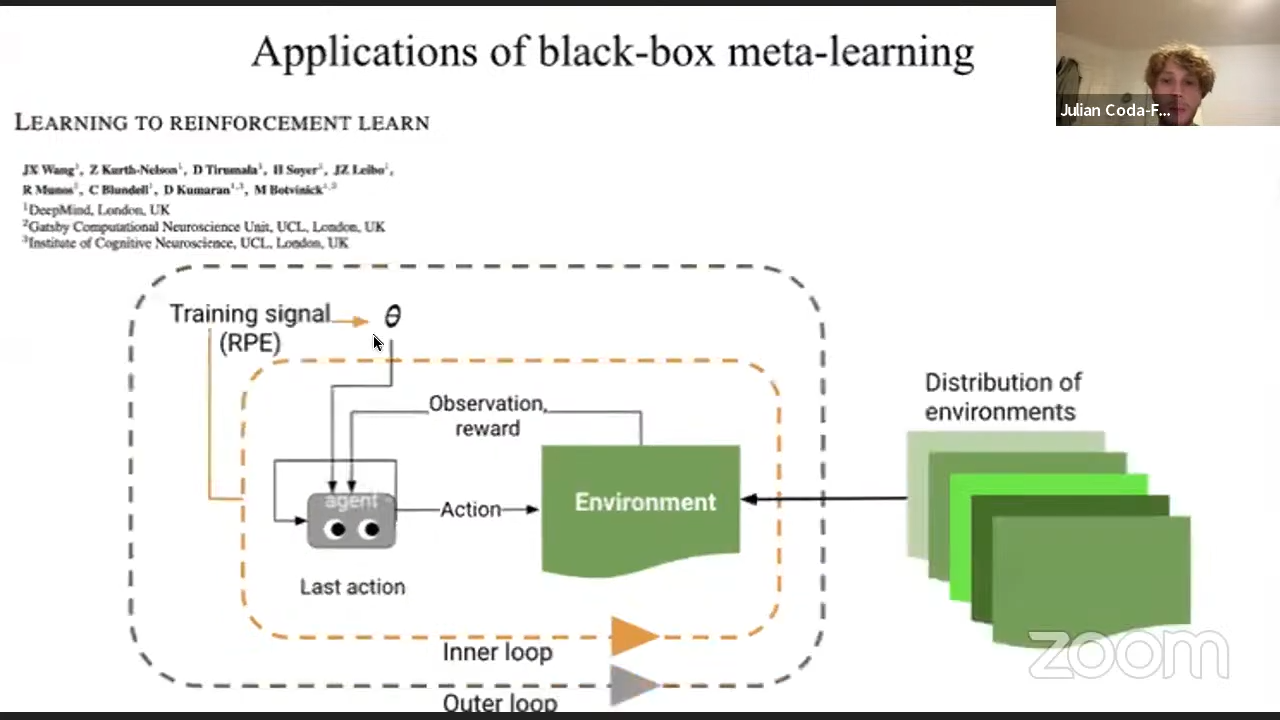
The authors follow up with another work, implementing a version of the “Harlow task” experiment and observe very similar meta-learning phenomenon to the original results with monkeys as compared to an artificial RL agent.

How does black-box meta-learning relate to language modelling?

Recall that in black-box meta-learning, we employ the forward pass of an RNN/sequence model as the learning “inner loop” and backpropogate over multiple tasks as the meta-learning “outer loop.” Looking more closely, the framework of black-box meta learning framework looks quite similar to language modelling where instead the tokens are individual inputs, where the outer-loop is training over various text corpuses.

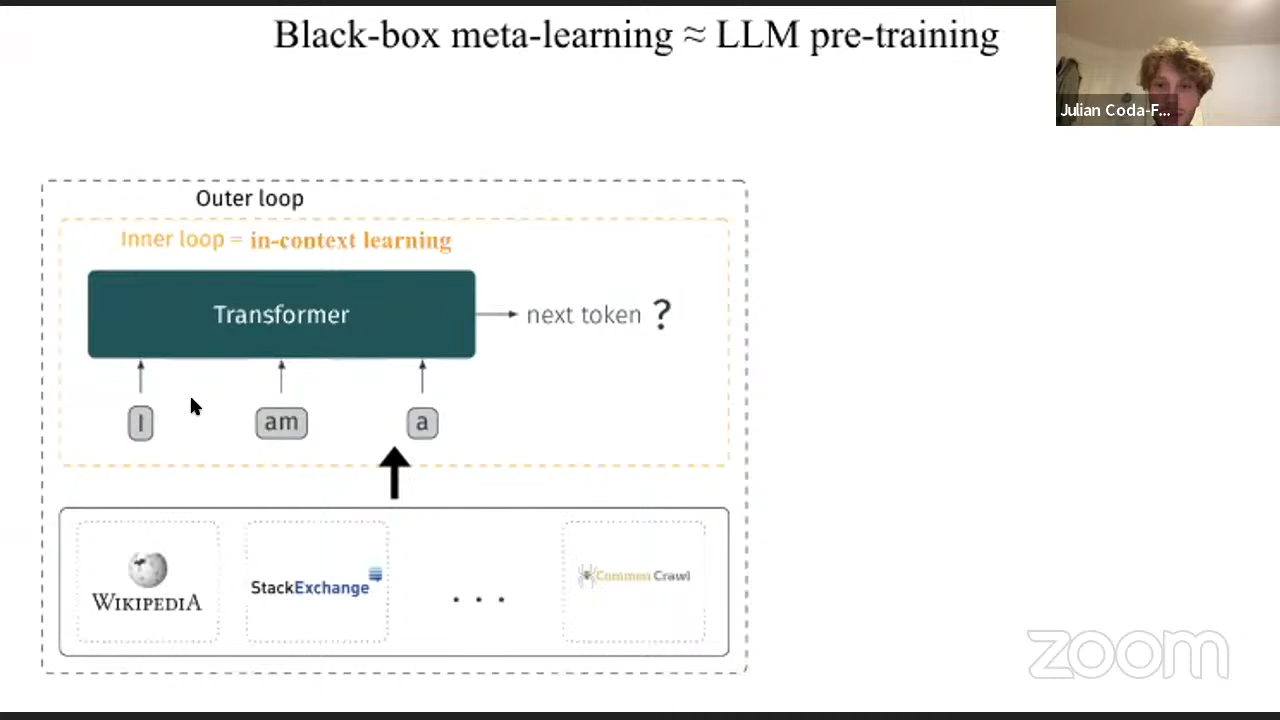
This shapes an intuition: once we replace the RNN with a transformer, that the phenomenon of “in-context learning”, we observe in the “inner loop” forward pass might be a real kind of learning and has properties of Bayesian inference we discussed previously from black-box meta learning!

Coda-Forno et al. (2023) examine to a deeper degree by trying to perform what they coin as “meta-in-context” learning. In-context learning (also termed few-shot prompting) is a phenomenon where model performance improves from being given a few exemplars within the prompt during inference: the authors here explore whether ICL itself can be improved using in-context learning as the learning mechanism itself, essentially conducting both loops of meta-learning fully in context. They show strong results comparable with fine-tuning, showing how LLMs can be adapted and learn purely at inference time.

Conclusion

In summary, Julian introduces us to the field of meta-learning and its foundations in cognitive science, and how “learning to learn” allows us to efficiently learn from data and generalize across tasks. He takes us through applications and connections to human and animal cognition and dives deeper into a specific branch of meta-learning, specifically black-box meta-learning. He discusses how this type of meta-learning implicitly yield strong theoretical guarantees in addition to having benefits with respect to model choice and tractability. Julian connects language modelling to the structured framework of black-box meta-learning, suggesting that the reason for phenomena like in-context learning might attributed to the Bayesian guarantees resulting from black-box meta-learning. Finally, he presents some promising results for meta-learning fully in the context of LLMs, which is very promising for adapting LLMs at inference time without retraining.

“Learning (to learn) useful representations in a structured world” (Jane Wang)

Work in progress!